Ergodic theory of the Burgers equation with random force

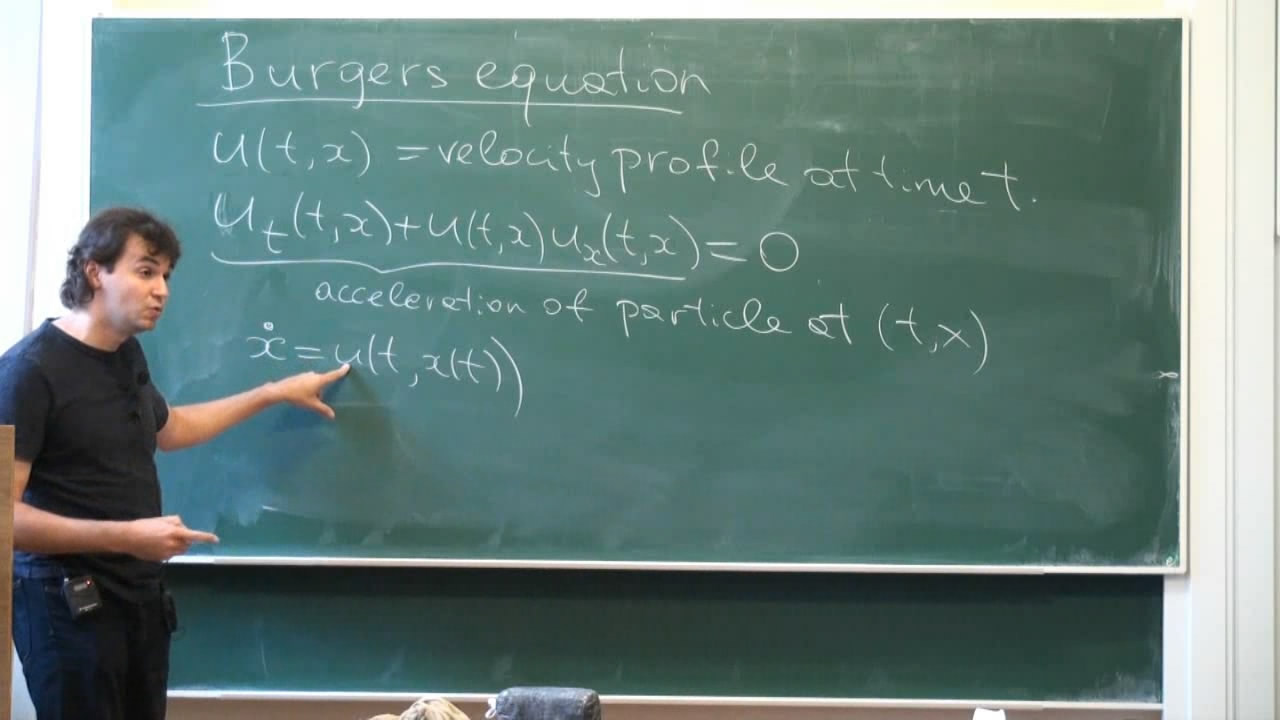
The Burgers equation is one of the basic hydrodynamic models that describes the evolution of velocity fields of sticky dust particles. When supplied with random forcing it turns into an infinite-dimensional random dynamical system that has been studied since late 1990's. The variational approach to Burgers equation allows to study the system by analyzing optimal paths in the random landscape generated by random force potential. Therefore, this is essentially a random media problem. For a long time only compact cases of Burgers dynamics on the circle or a torus were understood well. However, recently a lot of progress was achieved for noncompact cases with forcing based on Poissonian point field.

The course is naturally split into three parts. In the first part I will recall basics on the Burgers equation and explain the central ergodic result, so called One Force --- One Solution (1F1S) Principle, for Burgers dynamics with random force in the compact case. The second part will be devoted to localization and 1F1S in the quasi-compact case where the random forcing decays to zero at infinity. In the third part I will talk about 1F1S for the case of the forcing that is stationary in space-time and has no decay at infinity. This part is based on techniques that have been developed for last-passage percolation and related models. It involves Kesten's concentration inequality, greedy lattice animals, and other tools of modern probability theory.

Курс прочитан в рамках St. Petersburg School in Probability and Statistical Physics.