Schauder bases geometry in Hilbert spaces
Курс ХитПредмет:
- Математика
Лектор:
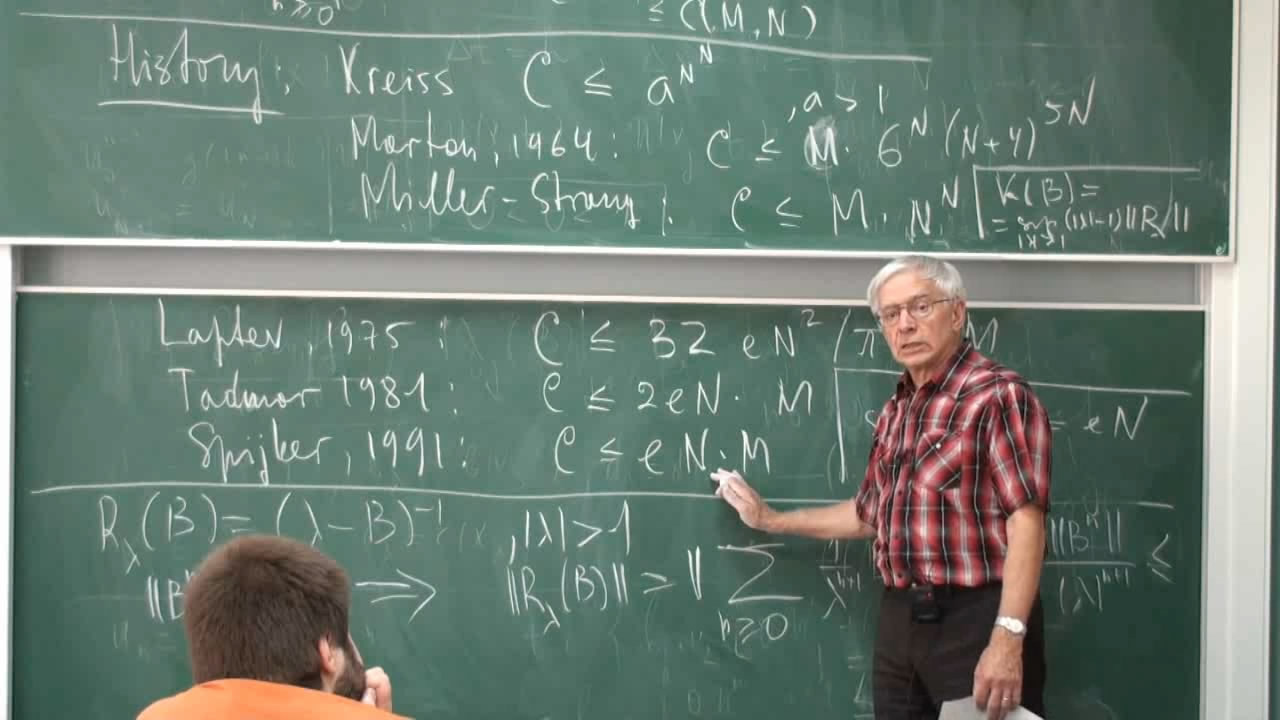
Numerical characteristics of Hilbert space bases play an important role in Harmonic Analysis and its applications, from weighted singular integrals through numerical matrix analysis. In this short course, we focus on problems around the behaviour of the basis and unconditional basis constants, as well as Fourier-Hadamard multipliers. The McCarthy-Schwartz inequality is revisited, and its sharpness is derived from results by Spijker, Tracogna and Welfert. A BeurlingDeny theory of abstarct Besov-Dirichlet spaces is traced, culminating in a complete description of Fouruer-Muckenhoupt multipliers for weighted L^2 spaces with a Schoenberg weight. Applications to matrix analysis is discussed, in particular to the Kreiss matrix theorem.
Лекции курса
3